Derivative and Backpropagation
Introduction
This post revisits the fundamental concepts of derivatives and highlights their crucial role in training neural networks. We will begin by methodically calculating the derivative of a mathematical expression, refreshing our understanding of its principles and implications.
Along the way, we will cover the chain rule, a critical technique for computing derivatives of composite functions, and explore how it is applied during backpropagation.
After covering these basics, we will put the concepts into practice using an incomplete implementation of Andrej Karpathy’s Micrograd Library, performing a manual backpropagation process on a simple neural network.
If you are already well-versed in Calculus, the chain rule, and their applications in neural networks, feel free to skip ahead.
Derivative
A Neural Network Perspective
When I first revisited the core concepts of derivatives to understand how a neural network trains itself, all sorts of definitions I had learned in high school came flooding back to me:
- Instantaneous rate of change
- Slope of the tangent line
- Sensitivity of a function’s change with respect to its input
These are all valid descriptions of derivatives, and we generally have a good understanding of how each ties to the underlying concept. However, for me, the last description—sensitivity of change—resonates most clearly when thinking about neural network training.
In essence, a neural network is built upon matrix multiplications of input data, weights, and biases. Training involves iteratively adjusting these parameters to minimize the loss function and better represent the data. Derivatives play a crucial role here, as they measure how sensitive the loss function is to each parameter, guiding their updates through optimization algorithms like gradient descent.
Definition
As described above, the difference quotient measures how the function’s output changes as its input ($x=a$) changes by $h$. \(f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}\)
- $f’(a)$ : The derivative of $f(a)$ at $x=a$
- $h$ : Small change in $a$
Example
Example 1.1
Let’s play around with the mathematical expression: \(y = 7x^2 + 6x + 3\)
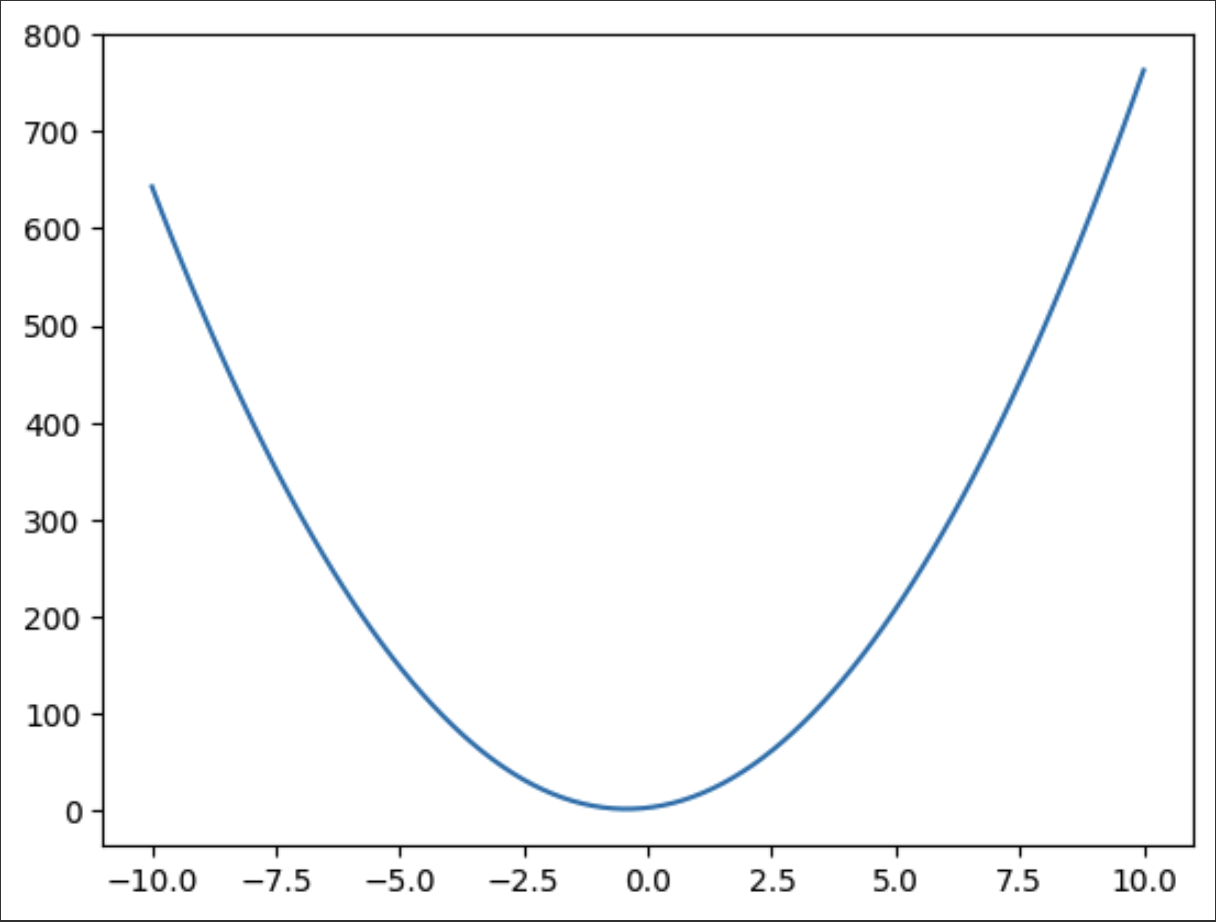
Using a power rule, we come up with: \(y' = 14x + 6\)
However, let’s use the derivative formula to compute the derivative when $x=5$.
1
2
3
4
5
6
7
def f(x):
return (7 * x**2) + (6 * x) + 3
x = 5
h = 0.0001
print((f(x+h) - f(x)) / h) # Should be y' = 14(5) + 6 = 76
1
76.00069999995185
The derivative of 76.0 tells us, for a small change in $x$, the value of $y$ increases by approximately 76 times the $x$.
\[Δy ≈ y' ⋅ h = 76 ⋅ 0.0001 = 0.0076\]
1
2
3
4
diff = f(x+h) - f(x)
derivative = (f(x+h) - f(x)) / h
print(f"Difference by h: {diff}, derivative * h: {derivative * h}")
1
Difference by h: 0.007600069999995185, derivative * h: 0.007600069999995185
Example 1.2
This time, let’s compute a partial derivative of given expression \(y = a * b + c\)
Partial derivatives:
With respect to $a$: \(\frac{dy}{da} = b\)
With respect to $b$: \(\frac{dy}{db} = a\)
With respect to $c$: \(\frac{dy}{dc} = 1.0\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def f(a, b, c):
return a * b + c
a = 2.0
b = -3.0
c = 10.0
h = 0.0001
constant = f(a, b, c)
# With respect to a: -3.0
print(f"df/da: {(f(a+h, b, c) - constant) / h}")
# With respect to b: 2.0
print(f"df/db: {(f(a, b+h, c) - constant) / h}")
# With respect to c: 1.0
print(f"df/dc: {(f(a, b, c+h) - constant) / h}")
1
2
3
df/da: -3.000000000010772
df/db: 2.0000000000042206
df/dc: 0.9999999999976694
Manual Backpropagation on Micrograd
Micrograd is an auto-differentiation engine designed to work with scalar values. For the purpose of manually performing gradient calculations and backpropagation, we will utilize a simplified and incomplete implementation of the Value class.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Value:
def __init__(self, data, _children=(), _op='', label=''):
self.data = data
self.grad = 0.0
self._prev = set(_children)
self._op = _op
self.label = label
def __repr__(self):
return f"Value(data={self.data})"
def __add__(self, other):
out = Value(self.data + other.data, (self, other,), '+')
return out
def __mul__(self, other):
out = Value(self.data * other.data, (self, other,), '*')
return out
Using the Value class, we will create a tiny network of:
1
2
3
4
5
6
7
a = Value(2.0); a.label = 'a'
b = Value(-3.0); b.label = 'b'
c = Value(10.0); c.label = 'c'
e = a * b; e.label = 'e'
d = e + c; d.label = 'd'
f = Value(-2.0); f.label = 'f'
L = d * f; L.label = 'L'

In this neural network, our goal is to compute the derivative of $L$ (the loss) with respect to the variables or weights in the expression. Why is this important? It helps us understand how much each parameter contributes to changes in the output. This concept will become clearer as we explore the loss function and gradient descent. For now, focus on the idea that our objective is to compute the gradient at each node.
Now, let’s compute derivative from the last layer (i.e., output layer) of the neural network.
Derivative of $L$:
- With respect to $L$: \(\frac{dL}{dL} = 1.0\)
- With respect to $f$: \(\frac{dL}{df} = d\)
- With respect to $d$: \(\frac{dL}{dd} = f\)
Remember to use Chain Rule to express the derivative of the composition of two differentiable functions.
\[\frac{dz}{dx} = \frac{dz}{dy} ⋅ \frac{dy}{dx}\]Therefore, since $L = f(c + e)$:
- With respect to $c$: \(\frac{dL}{dc} = \frac{dL}{dd} ⋅ \frac{dd}{dc} = f ⋅ 1.0 = f\)
- With respect to $e$: \(\frac{dL}{de} = \frac{dL}{dd} ⋅ \frac{dd}{de} = f ⋅ 1.0 = f\)
- With respect to $a$: \(\frac{dL}{da} = \frac{dL}{dd} ⋅ \frac{dd}{de} ⋅ \frac{de}{da} = f ⋅ 1.0 ⋅ b = bf\)
- With respect to $b$: \(\frac{dL}{db} = \frac{dL}{dd} ⋅ \frac{dd}{de} ⋅ \frac{de}{db} = f ⋅ 1.0 ⋅ a = af\)
Based on this derivation, we can manually set the gradient of each node to:
1
2
3
4
5
6
7
a.grad = 6.0
b.grad = -4.0
c.grad = -2.0
e.grad = -2.0
d.grad = -2.0
f.grad = 4.0
L.grad = 1.0

And with that, we have just completed our first backpropagation!
Backpropagation by definition is a gradient estimation method which computes the gradient of a loss function (for our examle $L$) with respect to the weights of the network. This process involves chain rule to break the computation into pieces (remember how we multiplied the local gradient to the global gradient propagated from the output layer).
Final Step: Optimization
Now, we will see how we can increase the output $L$ by nudging the variables by their gradients.
1
2
3
4
5
6
7
8
9
10
a.data += 0.01 * a.grad
b.data += 0.01 * b.grad
c.data += 0.01 * c.grad
f.data += 0.01 * f.grad
e = a * b
d = e + c
L = d * f
print(L.data)
1
-7.286496
Key Observations
- Nodes with a positive gradient indicate that increasing the value of the corresponding node will result in an increase in \(L\) (positive correlation).
- Nodes with a negative gradient indicate that increasing the value of the corresponding node will result in an decrease in \(L\) (negative correlation).
Remember that gradient represents the rate of change of \(L\) with respect to the variable (direction of steepest ascent).
Gradient is updated by: \(x_t = x_{t-1} + \eta \cdot \frac{\partial L}{\partial x}\)
- $\eta$: Learning Rate
- $\frac{\partial L}{\partial x}$: Gradient of \(L\) with respect to \(x\)
Conclusion
We have explored the fundamental concepts of derivatives and their role in training neural networks. Along the way, we delved into the chain rule, manually computed gradients, and performed backpropagation using Micrograd. Finally, we touched on an optimization technique, providing a solid foundation for understanding gradient descent.