Building a Multilayer Perceptron (MLP) from Scratch

Introduction

The past two posts have laid the groundwork for understanding the mathematical underpinnings of neural networks. In each post, we briefly covered:

• Gradient and Derivative: The concept of derivatives and their application in neural networks during backpropagation.
• Linearity and Linear Transformation: The concept of linearity and linear transformation and why neural networks need non-linear activation functions (and how a deeply stacked linear model is equivalent to a single linear model).

While these two posts have provided the necessary mathematical foundation, I was particularly excited working on today’s post because we will be getting our hands dirty with some actual code! This time, we will be building a Multilayer Perceptron (MLP) and train the network from scratch by:

• Adding more functionality to the Value class to support more operations (e.g., exponential, tanh, automatic differentiation, etc.)
• Constructing a simple 2-layer MLP to solve the XOR problem
• Implementing the gradient descent algorithm to optimize the MLP parameters
• Using PyTorch to build the same MLP model and compare the performance

Value Class Revisited

So far, the Value class has implemented basic arithmetic operations: addition and multiplication. While these operations are sufficient for implementing simple linear models and demonstrating how neural networks fundamentally rely on matrix multiplication, we now need to extend the class to support:

• Non-linear activation functions (e.g., tanh)
• Additional arithmetic operations (e.g., division, subtraction, power)
• Automatic differentiation for backpropagation
• Exponential functions for advanced activation functions

Let’s first take a look at the updated Value class:

import math

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0
        self._backward = lambda: None # This closure will be `None` to a leaf node.
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        return f"Value(data={self.data})"

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data, (self, other), '+')

        def _backward():
            self.grad += 1.0 * out.grad
            other.grad += 1.0 * out.grad
        out._backward = _backward

        return out

    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data, (self, other), '*')

        def _backward():
            self.grad += other.data * out.grad
            other.grad += self.data * out.grad
        out._backward = _backward

        return out

    def __pow__(self, other):
        assert isinstance(other, (int, float)), "only supporting int/float powers for now"
        out = Value(self.data ** other, (self, ), f'**{other}')

        def _backward():
            self.grad += other * (self.data ** (other - 1)) * out.grad
        out._backward = _backward

        return out

    def __rmul__(self, other):
        return self * other

    def __truediv__(self, other):
        return self * other**-1

    def __neg__(self):
        return self * -1

    def __sub__(self, other):
        return self + (other * -1)

    def __radd__(self, other):
        return self + other

    def tanh(self):
        x = self.data
        t = (math.exp(2 * x) - 1) / (math.exp(2 * x) + 1)
        out = Value(t, (self, ), 'tanh')

        def _backward():
            self.grad += (1 - t**2) * out.grad
        out._backward = _backward

        return out

    def exp(self):
        x = self.data
        out = Value(math.exp(x), (self, ), 'exp')

        def _backward():
            self.grad += out.data * out.grad
        out._backward = _backward

        return out

    def backward(self):
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)

        self.grad = 1.0
        for node in reversed(topo):
            node._backward()

I will not go through every details of the code because the implementation is straightforward and Andrej Karpathy does a great job explaining in the lecture. However, I will highlight some of the key functionalities that we have added to the class.

backward()

The backward() method implements reverse mode automatic differentiation (commonly known as backpropagation). It computes gradients for all nodes in the computational graph, starting from the node where backward() is called.

To illustrate the advantage of this automated approach, let’s compare it with manual backpropagation.

In manual backpropagation, we apply the chain rule to compute derivatives with respect to each node. For instance, to calculate how a change in node $e$ affects our final output $L$, we would compute:

\[\frac{\partial L}{\partial e} = \frac{\partial L}{\partial d} \cdot \frac{\partial d}{\partial e} = -2.0 \cdot 1.0 = -2.0\]

# Manually set the gradient for node e.
e.grad = -2.0

While manual computation is feasible for small networks, it becomes impractical for real-world neural networks that often contain thousands or millions of parameters.

The solution leverages the fact that neural networks form a directed acyclic graph (DAG). By performing a topological sort on this graph, we can systematically propagate gradients through the network by calling each node’s _backward() method in reverse topological order.

Below is an example of what the reversed topological sort might produce for our computational graph:

[
    Value(data=-8.00), # L
    Value(data=-2.0),  # f
    Value(data=4.0),   # d
    Value(data=10.0),  # c
    Value(data=-6.0),  # e
    Value(data=-3.0),  # b
    Value(data=2.0),   # a
]

_backward()

The _backward() method is a closure that computes the gradient of the current node with respect to its parents. This method is arguably the most important function of the class so it is important to understand the mathematical and memory aspects of this function.

Let’s use this example below to understand exp()’s _backward() method:

def exp(self):
    x = self.data
    out = Value(math.exp(x), (self, ), 'exp')

    def _backward():
        self.grad += out.data * out.grad
    out._backward = _backward

return out

a = Value(2.0);             a.label='a'
b = Value(4.0);             b.label='b'
c = a * b;                  c.label='c'
o = c.exp();                o.label='o'

o.backward()

Mathematical Perspective

_backward() functions in every operations are adding the product of local and global derivative. More precisely, we are interested in computing the local derivative (for exp() the derivative of $e^x$) and the global derivative (the gradients from the output layer until current node).

As derivative of $e^x$ is just $e^x$ itself, the _backward() function of exp() adds the product of out.data (local derivative) and out.grad (gradient so far from the output layer).

Memory Perspective

The way _backward() works might seem mysterious at first - how can a closure stored in a child node modify its parent’s gradient? Let’s break this down by looking at memory references:

# Example setup
a = Value(2.0)      # Parent node
b = a.exp()         # Child node with _backward closure

When we create a new operation (like exp()), we:

1. Create a new output node
2. Define a _backward() function that “remembers” both the output and input nodes
3. Store this function in the output node

Here’s a simplified trace showing how the memory references work:

class Value:
    # Keep other codes unchanged.

    def exp(self):
        out = Value(math.exp(self.data), (self,), 'exp')
    
        def _backward():
            # This closure maintains references to both:
            # - self (the input node)
            # - out (the output node)
            print(f"out: {out.label}({id(out)}) setting grad of self: {self.label}({id(self)})") # Added to print memory address
            self.grad += out.data * out.grad
        out._backward = _backward

        return out
    
    def backward(self):
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)

        self.grad = 1.0
        for node in reversed(topo):
            print(f"current node: {node.label}({id(node)})") # Added to print memory address of current node
            node._backward()

# Initialize a = 2.0 and b = exp(2.0)
a = Value(2.0);     a.label='a'
b = a.exp();        b.label='b'

b.backward()

When backward() is called, it walks through the nodes in reverse order, and each _backward() function still has access to its original references. We can verify this by printing the memory addresses:

current node: b(132272235835504)
out: b(132272235835504) setting grad of self: a(132272235837136)
current node: a(132272235837136) # `a` is a leaf node so _backward() is None

This shows how each _backward() function maintains its connection to both the node it was created in and the node(s) it needs to update, allowing gradients to flow backward through the network.

tanh()

We have learned about linearity and linear transformation in the previous post. And also covered why we need non-linear activation function to train deep neural networks. The tanh function (also known as the hyperbolic tangent) is one of the most commonly used activation functions and it is defined as:

\[\text{tanh}(x) = \frac{sinh(x)}{cosh(x)} = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} = \frac{e^{2x} - 1}{e^{2x} + 1}\]

I will not go through the mathematics behind the tanh nor its derivative because it is not the focus of this post. However, it is important to understand that the tanh function maps any real number to the range [-1, 1].

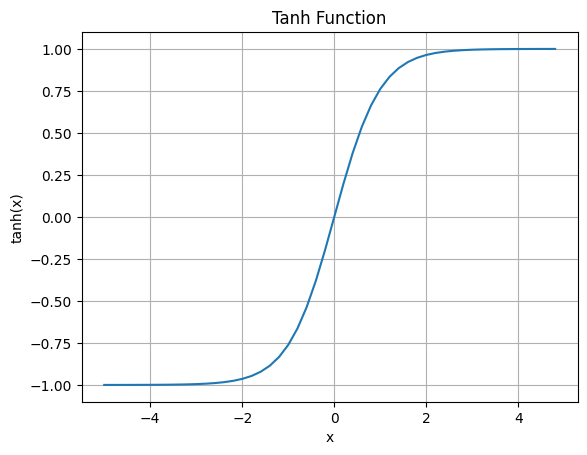
The the derivative of tanh is:

\[\frac{d}{dx} \text{tanh}(x) = 1 - \text{tanh}^2(x)\]

Therefore, the tanh() function in the Value class computes the tanh of the input data and defines a _backward() function that updates the gradient of the input node based on the derivative of tanh.

def tanh(self):
    x = self.data
    t = (math.exp(2 * x) - 1) / (math.exp(2 * x) + 1)
    out = Value(t, (self, ), 'tanh')

The example below shows that the _backward() function of tanh() updates the gradient of the input node based on the derivative of tanh:

a = Value(3.0);     a.label='a'
b = a.tanh();       b.label='b'

b.backward()

a.grad is updated to 0.0099 and this can be verified by $1 - 0.9951^2 = 0.0099775$.

Building MLP

Now, the Value class has all the necessary functionalities to create a Multilayer Perceptron. Value class will be the core building block of the network and the network can be broken into three major parts: neuron, layer, MLP.

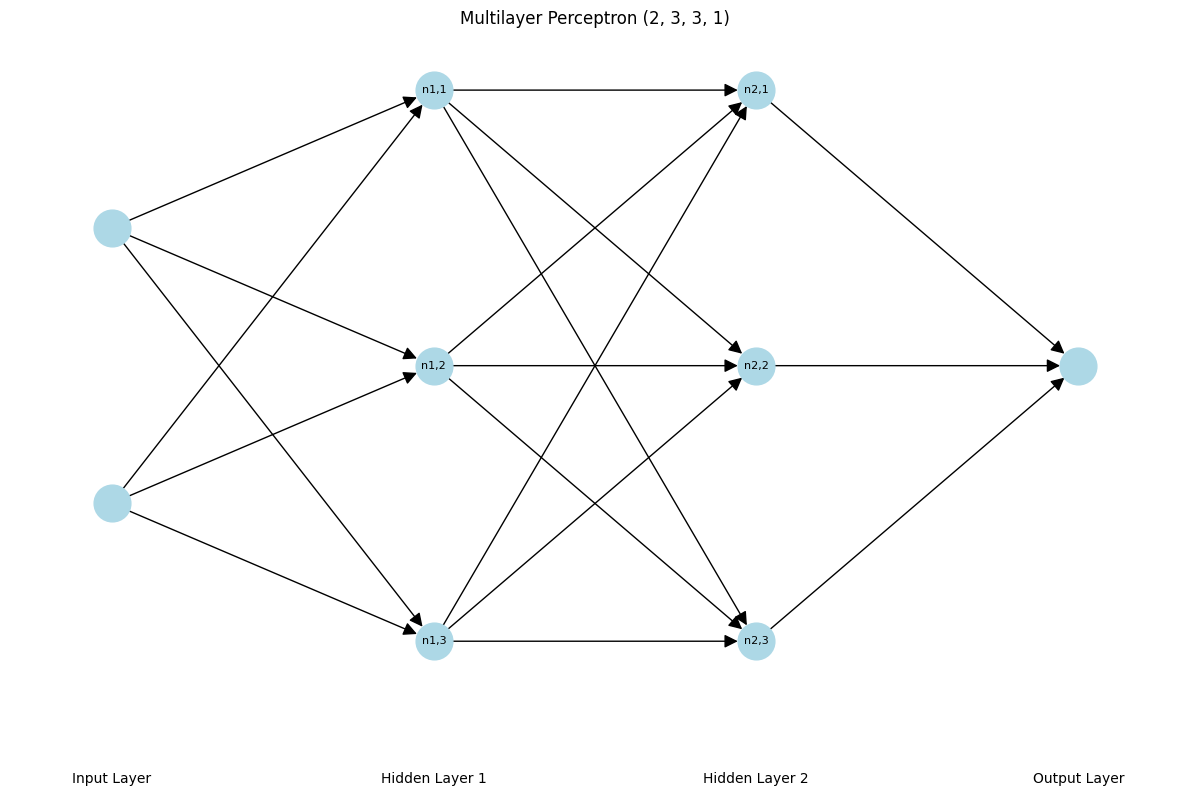
Neuron

A neuron is a computational unit that processes inputs by applying a weighted sum of those inputs, adds a bias, and passes the result through an activation function to produce an output. In the diagram above, nodes denoted as $n_{i,j}$ are neurons.

So for example, Neuron $n_{1, 1}$ will compute the weighted sum of input vector with size of [2, 1] (vectors are set to arbitrary values) and $\sigma$ is the tanhactivation function:

\[\begin{aligned} weight &= \begin{bmatrix} 5 & 10 \\ \end{bmatrix}, \quad input = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad bias = \begin{bmatrix} 20 \\ \end{bmatrix} \end{aligned}\] \[\begin{aligned} \sigma (\begin{bmatrix} 5 & 10 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} + \begin{bmatrix} 20 \\ \end{bmatrix}) \end{aligned} = \sigma (\begin{bmatrix} 25 \\ \end{bmatrix})\]

Now taking a look at the Neuron class, we can see that it initializes the weights and bias with random values between -1 and 1. And the __call__ method computes the weighted sum of the inputs, adds the bias, and applies the tanh activation function. nin is the number of inputs that the neuron takes so picture nin amounts of edges coming into the neuron.

class Neuron:
    def __init__(self, nin):
        self.w = [Value(random.uniform(-1, 1)) for _ in range(nin)]
        self.b = Value(random.uniform(-1, 1))

    def __call__(self, x):
        act = sum((wi * xi for wi, xi in zip(self.w, x)),self.b)
        out = act.tanh()

        return out

    def parameters(self):
        return self.w + [self.b]

Layer

A layer is a collection of neurons that processes (weighted summation, adding bias, and applying activation function) the same input in parallel.

From the diagram above, both Hidden Layer 1 and Hidden Layer 2 contain 3 neurons each. Therefore, the Layer class takes the number of neurons nout as an input and initializes a list of neurons with the size of nin.

class Layer:
    def __init__(self, nin, nout):
        self.neurons = [Neuron(nin) for _ in range(nout)]

    def __call__(self, x):
        out = [n(x) for n in self.neurons]
        return out[0] if len(out) == 1 else out

    def parameters(self):
        return [p for Neuron in self.neurons for p in Neuron.parameters()]

So, if we were to create a layer with 3 neurons which takes 2 inputs each, we will be initializing as:

layer = Layer(2, 3)

print(len(layer.neurons)) # Number of neurons in the layer: 3
print(len(layer.neurons[0].w)) # Number of weights for the first neuron: 2

If you recall the Implication of Matrix Mutiplication section from the previous post, you might notice that $\vec{y} = W\vec{X} + \vec{b}$ (under the hood) was a mathematical expression of hidden layer’s computation. Using the mathematical example from above, Layer computes the weighted sum in parallel for each neuron:

\[\begin{aligned} weight &= \begin{bmatrix} 5 & 10 \\ 15 & 20 \\ 25 & 30 \\ \end{bmatrix}, \quad input = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad bias = \begin{bmatrix} 20 \\ 30 \\ 40 \\ \end{bmatrix} \end{aligned}\] \[\begin{aligned} \sigma (\begin{bmatrix} 5 & 10 \\ 15 & 20 \\ 25 & 30 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} + \begin{bmatrix} 20 \\ 30 \\ 40 \\ \end{bmatrix}) \end{aligned} = \sigma (\begin{bmatrix} 25 \\ 45 \\ 65 \end{bmatrix})\]

MLP

Now the term multilayer perceptron should be clicking!

MLP is a neural network composed of multiple layers of neurons, where each neuron in a layer is fully connected to neurons in the adjacent layers. It consists of an input layer, one or more hidden layers, and an output layer.

class MLP:
    def __init__(self, nin, nout):
        sz = [nin] + nout
        self.layers = [Layer(sz[i], sz[i+1]) for i in range(len(nout))]

    def __call__(self, x):
        for layer in self.layers:
            x = layer(x)

        return x

    def parameters(self):
        return [p for layer in self.layers for p in layer.parameters()]

MLP class takes in two arguments:

• nin: Number of inputs in integer
• nout: Architecture of the network in list

For example, if we want to create a MLP with architecture of [2, 3, 3, 1], we will initialize as:

mlp = MLP(2, [3, 3, 1])

Iteration of self.layers will create 3 Layer objects with the size of [2, 3], [3, 3], and [3, 1] respectively.

mlp = MLP(2, [3, 3, 1])

for layer in mlp.layers:
    print(f"layer size: {len(layer.neurons)}, neuron size: {len(layer.neurons[0].w)}")

layer size: 3, neuron size: 2
layer size: 3, neuron size: 3
layer size: 1, neuron size: 3

The __call__ method will then iterate through each layer and compute the output of the next layer. x will be changing its value and dimension as it moves through the network.

Using MLP to Solve XOR Problem

Now that we have built the MLP, let’s see how it performs on the XOR problem.

Create the dataset and Initialize MLP

xs = [
    [0, 0],
    [0, 1],
    [1, 0],
    [1, 1],
]
ys = [0, 1, 1, 0]

n = MLP(2, [3, 3, 1])

We create a feature set of xs and a target set of ys. Recall that the XOR problem is a binary classification problem (output is either 0 or 1) which outputs True when the inputs are different and False when the inputs are the same.

A simple MLP architecture of [2, 3, 3, 1] is sufficient to solve the XOR problem.

Train the MLP using Gradient Descent

for epoch in range(1, 1001): # 1000 epochs
    # forward pass
    ypred = [n(x) for x in xs]
    loss = sum((yout - ygt)**2 for ygt, yout in zip(ys, ypred))

    # backward pass
    for p in n.parameters():
        p.grad = 0.0
    loss.backward()

    # update
    for p in n.parameters():
        p.data += -0.1 * p.grad

    # Print the loss every 100 epochs
    if epoch == 1 or epoch % 100 == 0: 
        print(f"epoch: {epoch}, loss: {loss.data}")

This is where the magic happens!

We iterate through the dataset multiple times (epochs) and update the weights and biases of the neurons through the gradient descent algorithm.

Forward Pass

We store the the predicted output of the MLP for each data point in ypred. Initially, ypred should be a list of 4 Value objects which poorly represents the target set ys.

Our objective is to compare how well the MLP is able to predict the target set ys. To do this, we can compute the Sum of the Squared Errors (SSE) for each data point which will give us a single value that represents the total error of the model (loss function).

Backward Pass

Gradient Reset

Pay close attention to the p.grad = 0.0 line. Here, we are setting the gradient of every parameters to 0.0 to prevent the Gradient Accumulation.

Gradient Accumulation is a phenomenon where the gradients of multiple iterations are accumulated, leading to incorrect updates of the parameters.

Remember from the Gradient post that the gradient represents the steepest ascent of the loss function. However, without resetting the gradient to 0.0 at each iteration, the gradient will accumulate and the ultimately store the sum of gradients of multiple forward-backward passes.

Gradient Computation

We run run automatic differentiation by calling backward() on the loss function to compute the gradient of the loss function with respect to the MLP parameters.

Update

With proper gradient computation, we can now iterate through each parameter and update the parameters of the MLP using the gradient descent algorithm.

Two things to note here:

• The learning rate of 0.1 is arbitrary and we can finetune this parameter to improve the performance of the model.
• We are shifting the parameters in the opposite direction of the gradient (-1 * learning rate * gradient) because we want to minimize the loss function.

The update loop is equivalent to the mathematical form from the Optimization Section of previous post: \(x_t = x_{t-1} + \eta \cdot \frac{\partial L}{\partial x}\)

Results

epoch: 1, loss: 6.711981193617913
epoch: 100, loss: 0.03429589147863325
epoch: 200, loss: 0.003300929666679126
epoch: 300, loss: 0.0021382588710887962
epoch: 400, loss: 0.0013622069772167259
epoch: 500, loss: 0.001007243870524433
epoch: 600, loss: 0.0011373601188590676
epoch: 700, loss: 0.0008423321709315533
epoch: 800, loss: 0.0006242304106202957
epoch: 900, loss: 0.0007032059394009284
epoch: 1000, loss: 0.0004800054226785212

print([round(yout.data) for yout in ypred]) # [0, 1, 1, 0]

From the loss values, we can see that the model is learning the input feature and the loss is decreasing (especially after 100 epochs).

PyTorch

import torch

torch.manual_seed(1337)

xs = torch.tensor([[0, 0], [0, 1], [1, 0], [1, 1]], dtype=torch.float32)
y = torch.tensor([0, 1, 1, 0], dtype=torch.float32)

w1 = torch.rand(3, 2);                  w1.requires_grad = True
b1 = torch.rand(3, 1);                  b1.requires_grad = True

w2 = torch.rand(3, 3);                  w2.requires_grad = True
b2 = torch.rand(3, 1);                  b2.requires_grad = True

w3 = torch.rand(1, 3);                  w3.requires_grad = True
b3 = torch.rand(1);                     b3.requires_grad = True

loss_fn = torch.nn.BCELoss()
optimizer = torch.optim.SGD([w1, b1, w2, b2, w3, b3], lr=0.1)

# forward
for epoch in range(1, 1001):
    # Forward pass
    z1 = w1 @ xs.T + b1  # (3, 2) @ (2, 4) + (3, 1) -> (3, 4)
    a1 = torch.tanh(z1)  # (3, 4)

    z2 = w2 @ a1 + b2  # (3, 3) @ (3, 4) + (3, 1) -> (3, 4)
    a2 = torch.tanh(z2)  # (3, 4)

    z3 = w3 @ a2 + b3  # (1, 3) @ (3, 4) + (1,) -> (1, 4)
    a3 = torch.sigmoid(z3)  # (1, 4)

    # Compute loss
    loss = loss_fn(a3.squeeze(), y)

    # Backward pass
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # Print loss
    if epoch % 100 == 0:
        predictions = (a3.squeeze() > 0.5).int()
        print(f"Epoch {epoch}, Loss: {loss.item()}, Prediction: {predictions}")

Above is the PyTorch implementation of the MLP. The major difference between the two implementations are:

• PyTorch implementation uses batch-wise forward and backward pass.
• PyTorch implementation uses optimizer to update the parameters of the MLP

Conclusion

That’s it! We have now built a simple MLP from scratch and seen how it can be used to solve the XOR problem. We applied our knowedlge in backpropagation and non-linearity to add functionlities to the Value class. And then used the class to build the MLP class by breaking it down to pieces (neurons and layers). Finally, we have learned how to use gradient descent to optimize the parameters of the MLP.

Resources

• The spelled-out intro to neural networks and backpropagation: building micrograd